文章內容
資料結構-使用C語言

演算法(Algorithms)是一解決問題(problems)的有限步驟程序。舉例來說,現有一問題為:判斷數字x 是否在一已排序好的數字串列s 中。其演算法為:從s 串列的第一個元素開始,依序的比較,直到x 被發現,或s 串列已達盡頭。假使x 被找到,則印出Yes;否則,印出No。
您是否常常會問這樣的一個問題:“他的程式寫得比我好嗎?”,答案不是因為他是班上第一名,因此他所寫出來的程式一定就是最好的,而是應該利用客觀的方法進行比較,而此客觀的方法就是複雜度分析(complexity analysis)。首先必須求出程式中每一敘述的執行次數(其中{和}不加以計算),將這些執行次數加總起來。然後求出其Big-O。讓我們來看以下六個範例:
1. 陣列元素相加(Add array members)
將陣列中每個元素相加後傳回總和。

2. 矩陣相乘(Matrix Multiplication)
矩陣相乘的定義如下:

3. 循序搜尋(Sequential search)
乃表示在一陣列中,由第1個元素開始依序搜尋,直到找到欲尋找的資料或陣列結束。

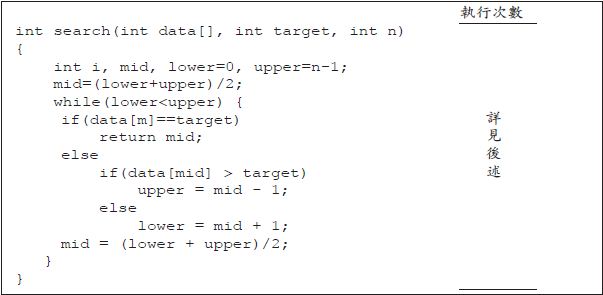
4. 二元搜尋(Binary search)
二元搜尋不同於循序搜尋,詳見後述,其效率較佳。
5. 費氏數列(遞迴的片段程式)
費氏數列表示第n 項為第n-1 項和第n-2 項的和。如0,1,1,2,3,5,8,13,... 是一費氏數列。

6. 費氏數列(非遞迴的片段程式)

如何去計算演算法所需要的執行時間呢?在程式或演算法中,每一敘述(statement)的執行時間為:(1) 此敘述執行的次數,及(2) 每一次執行所需的時間,兩者相乘即為此敘述的執行時間。由於每一敘述所需的時間必須實際考慮到機器和編譯器的功能,因此通常只考慮執行的次數而已。
循序搜尋(sequential search)的情形可分為三種,第一種為最壞的情形,此乃要搜尋的資料放置在檔案的最後一個,因此需要n 次才會搜尋到(假設有n 個資料在檔案中);第二種為最好的情形,此情形與第一種剛好相反,表示欲搜尋的資料在第一筆,故只要1次便可搜尋到;最後一種為平均狀況,其平均搜尋到的次數為
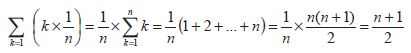
因此循序搜尋的Big-O為 O(n)。
二元搜尋(binary search)的情形和循序搜尋不同,二元搜尋法乃是資料已經皆排序好,因此由中間(mid)開始比較,便可知欲搜尋的資料(key)落在mid 的左邊還是右邊,再將左邊的中間拿出來與key 相比,只是每次要調整每個段落的起始位址或最終位址。
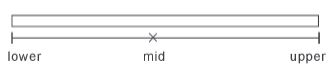
當key>data[mid] 時,mid=(lower+upper)/2,則lower=mid+1,upper 不變,如下所示:

當key

若此時key==data[mid] 時,便找到了欲尋找的資料,從上可知,當data 陣列的大小為32 時,其搜尋的點如下,並假設key 大於data 陣列中所有資料。

搜尋的次數為log32+1=6,此處的log 表示log2。資料量為128 個時,其搜尋的次數為log128+1,因此當資料量為n 時,其執行的次數為logn+1。底下有一二元搜尋與循序搜尋的比較表,假設key 大於陣列中所有元素值。

大略可知二元搜尋比循序搜尋好得太多了,其執行效率為O(logn) 。
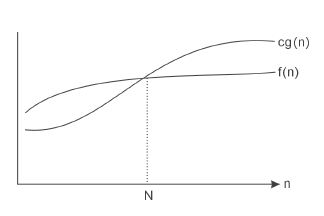
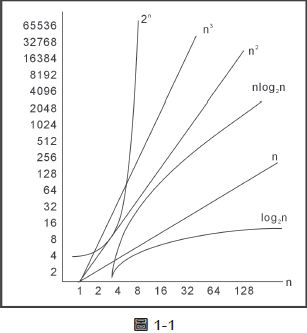
Big-O 的圖形表示如下:
一般常見的Big-O 有下列幾種情形:
1. O(1) 稱為常數時間(constant)
2. O(log n) 稱為次線性時間(sub-linear)
3. O(n) 稱為線性時間(linear)
4. O(n log n) 稱為n logn n
5. O(n2) 稱為平方時間(quadratic)
6. (n3) 稱為立方時間(cubic)
7. O(2n) 稱為指數時間(exponential)
8. O(n!) 稱為階層時間
當n > 16 時,其執行時間長短的順序如下:
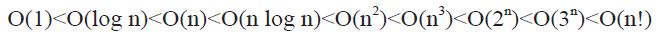
可由圖1-1或圖1-2 得知。我們可利用Big-O 來評量演算法的效率為何。當n 愈大時,更能顯示其間的差異。

【推薦閱讀】其它詳細內容請參閱「資料結構-使用C語言,蔡明志編著,全華圖書出版」。
